A full description of all the physics in the Henriques2015a release of the Munich model of galaxy formation is presented in the supplementary material of the main article (Henriques et al., 2015, MNRAS, 451, 2663) and can be downloaded separately here: L-Galaxies_Documentation.pdf
- Changes in the model with respect to Guo11
- Complete list of differential equations controlling galaxy formation physics:
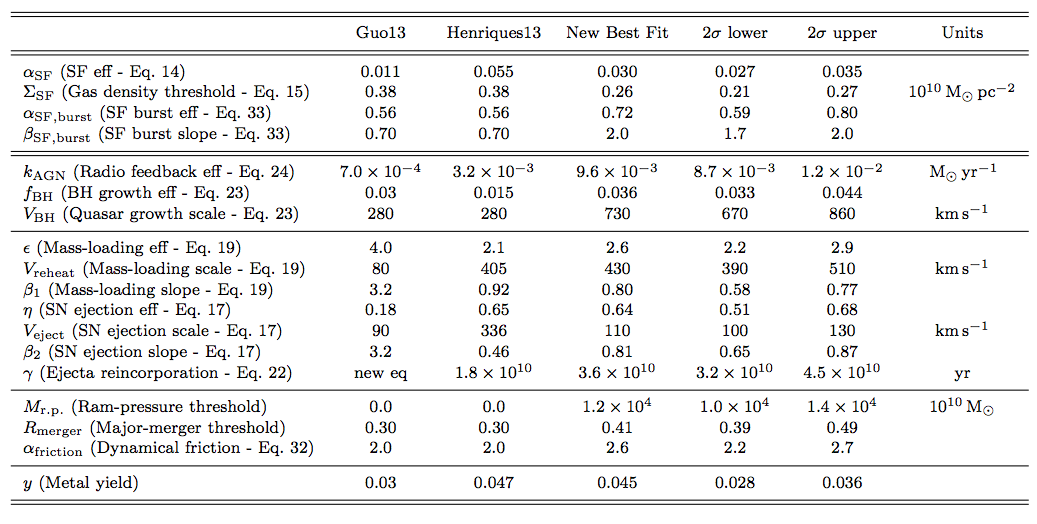
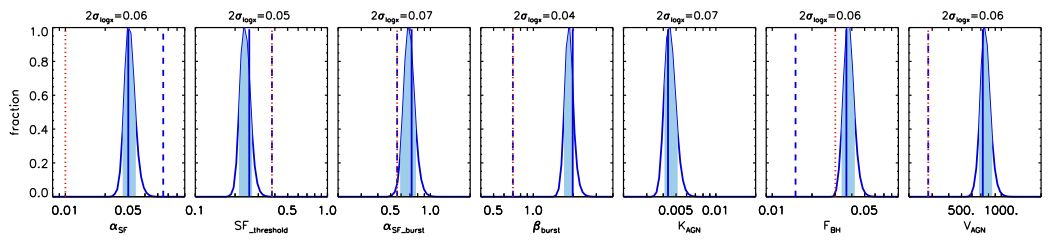
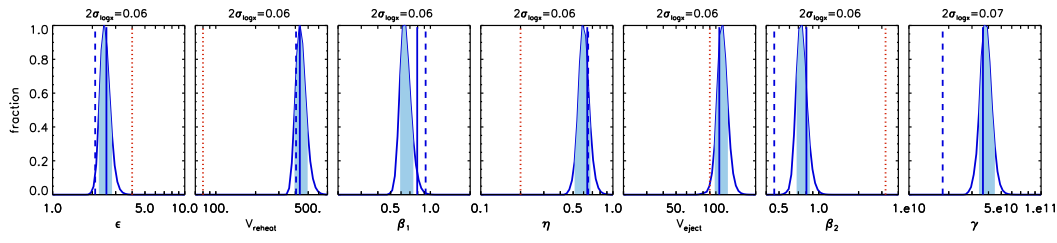
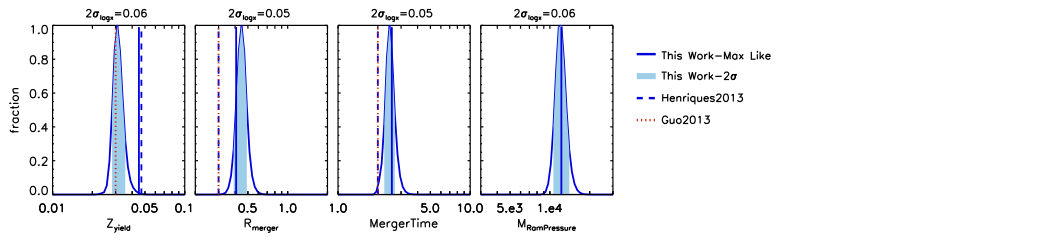
- Parameters controlling the efficiencies of galaxy formation physics:
All physical parameters were adjusted by fully exploring the highly-dimensional parameter space using Monte Carlo Markov Chain methods. The stellar mass function and the fraction of red galaxies from z=3 to z=0 were used as observational constraints.
The evolution of galaxy properties is computed on top of a scaled version of the Millennium and Millennium-II simulations to match the cosmological parameters from PLANCK Year 1.
Here is a schematic view of the box sizes and particle masses for the Millennium Simulation in different cosmologies:

In the current model, mainly four aspects of the physical modelling were adjusted with respect to Guo11:
\( \dot{M}_{\rm{ejec}}=-\frac{M_{\rm{ejec}}}{t_{\rm{reinc}}}\), where the reincorporation timescale is: \(t_{\rm{reinc}}=-\gamma' \frac{10^{10}M_{\odot}}{M_{200c}}\).
With respect to the previous implementation, where the reincorporation timescale was given by:
\(t_{\rm{reinc}}=\frac{1}{\gamma} t_{\rm{dyn,h}}\frac{200 \rm{km\;s^{-1}}}{V_{200c}}\),
the reincorporation of gas is faster in high mass galaxies and is significantly delayed in lower mass systems. This modification ensures that star formation is suppressed in low mass galaxies at early times and enhanced at z<2.
The following plot shows the differences between the Guo11 and the current reincorporation timescales as a function of virial velocity and redshift:

\(\dot{M}_{\star} = \alpha_{\rm SF}\frac{(M_{\rm gas}-M_{\rm crit})}{t_{\rm dyn,disk}}\) with \(M_{\rm{crit}}=M_{\rm{crit,0}}\left(\frac{V_{200c}}{200\,\rm{km\, s}^{-1}}\right) \left(\frac{R_{\rm{gas}}}{10\,\rm{kpc}}\right)\).
In comparison to previous works, the threshold in cold gas surface density for star formation (Mcrit,0) is reduced from \(3.8\times10^9 \rm\, M_{\odot}\) to \(2.6\times10^9\ \rm\, M_{\odot}\). This ensures that very low mass, gas dominated galaxies, continue to form stars.
The Guo11 model assumed that hot gas from satellite galaxies was stripped due to ram-pressure and tidal forces. At any given time, the stripping of a satellite was defined by the stronger of the two forces. We leave both implementations unchanged except that ram-pressure stripping is only turned on for groups with \(M_{\rm{200c}} \gt 10^{14}\rm\, M_{\odot}\).
This modification results in quenching timescales for satellites which are consistent with observations. While before galaxies in low mass groups had their gas removed and star formation stopped in \(\sim 2\, \rm{Gyr} \), satellites keep forming stars for as long as \(\sim 5 \, \rm{Gyr} \) in the new model.
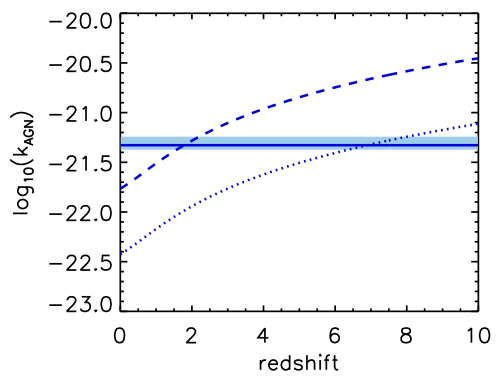
Observationally, the number density of galaxies around the knee
of the stellar mass function grows significantly below \(z=1\),
yet most \(M_*\) are quenched by \(z=0\). This behaviour is
reproduced in the new model by changing the AGN radio mode
feedback implementation and increasing its relative efficiency
at later times. The quiescent accretion of hot gas into the
central black hole is now given by:
\(\dot{M}_{\rm{BH}}=k_{\rm{AGN}}
\left(\frac{M_{\rm{hot}}}{10^{11}{\odot}}\right)\left(\frac{M_{\rm{BH}}}{10^8{\odot}}\right)\).
With respect to Guo11 we simply remove a dependence on
\( V_{200c}^3/M_{200c}\sim H (z)\).
Below is a comparison between the radio mode accretion efficiency in different
versions of our model.
|
|
Henriques et al. 2011 and Henriques et al. 2012 showed that,
at least in the context of the Munich model, stellar
populations that have significant emission from TP-AGB stars
in intermediate age populations appear required to reconcile
the observed evolution of the stellar mass and K-band luminosity
functions. For this paper, we therefore use the Maraston 2005, with
a Chabrier 2003 IMF, as our default stellar population
model.
In producing photometric catalogs, we also adjusted the high redshift
gas-to-dust ratio in our model. In Guo11 this ratio was
assumed to scale as \((1+z)^{-0.4}\) whereas we now adopt
\((1+z)^{-1}\). This change ensures that galaxies at very high redshift
have very little dust, as observed, and results in luminosity
functions for Lyman-break galaxies at \(z\ge5\) that match HST data
quite well. These effects will be discussed in a future paper
Clay et al. 2014. The optical depth of diffuse dust in
galactic disks is assumed to vary with wavelength as:
\(\tau_{\lambda}^{ISM}=
\left(\frac{A_{\lambda}}{A_v}\right)_{Z_{\odot}}
(1+z)^{-1}\left(\frac{Z_{\rm{gas}}}{Z_{\odot}}\right)^s
\times \left(\frac{\langle N_H\rangle}{2.1 \times10^{21}
{\rm{atoms}}\,{\rm{cm}}^{-2}}\right)\).
Here we just described the differential equations controlled by free parameters, the full list is given in the supplementary material provided in the link above.
The mass of stars formed quiescently is given by:
\(\dot{M}_{\star} = \alpha_{\rm SF}\frac{(M_{\rm gas}-M_{\rm crit})}{t_{\rm dyn,disk}}\) with \(M_{\rm{crit}}=M_{\rm{crit,0}}\left(\frac{V_{200c}}{200\,\rm{km\, s}^{-1}}\right) \left(\frac{R_{\rm{gas}}}{10\,\rm{kpc}}\right)\).
From the total mass of stars formed (M*), (1-R)M* is transferred to the stellar disk and the rest is assumed to be mass immediately returned to the cold gas by short lived massive stars. The threshold in cold gas surface density for star formation (Mcrit,0) is significantly reduced in the current version of the model in comparison to previous works.
The mass of stars formed violently due to the collision of cold gas during mergers is given by:
\({M}_{\star, \rm{burst}} = \alpha_{\rm{SF, burst}} \left(\frac{M_1}{M_2}\right)^{\beta_{\rm{SF, burst}}}M_{\rm{cold}}\)
In the current model only a small fraction of stars are formed during mergers (<10%). Therefore most of the predicted properties are insensitive to this process.
Supernova feedback is assumed to reheat cold gas into the hot phase and, if there is any leftover energy, eject hot gas into an external reservoir. The amount of energy available from dying massive stars after any star formation event is given by:
\(\Delta E_{\rm SN}=\epsilon_{\rm halo}\times\frac{1}{2}\Delta M_{\star}V_{\rm SN}^2\) where \(\epsilon_{\rm halo} =\eta\times \left[0.5+\left(\frac{V_{\rm max}}{V_{\rm eject}}\right)^{-\beta_{2}} \right]\)
From the total energy available some is used for reheating cold gas into the hot phase:
\(\Delta M_{\rm reheat}=\epsilon_{\rm disk}\Delta M_{\star}\) where \(\epsilon_{\rm disk}=\epsilon \times \left[0.5+\left(\frac{V_{\rm max}}{V_{\rm reheat}}\right)^{-\beta_{1}} \right]\)
From the total energy available, what is left after reheating is used to eject hot gas into an external reservoir:
\(\frac{1}{2}\Delta M_{\rm eject}V_{200c}^2=\Delta E_{\rm SN}-\Delta E_{\rm reheat}\)
Gas does not necessarily has to be ejected. This component simply holds the material that, at any given time, is too energetic to cool.
The ejected gas will later be reincorporated at a rate given by:
\( \dot{M}_{\rm{ejec}}=-\frac{M_{\rm{ejec}}}{t_{\rm{reinc}}}\), where the reincorporation timescale is: \(t_{\rm{reinc}}=-\gamma' \frac{10^{10}M_{\odot}}{M_{200c}}\).
This scheme, introduced in Henriques et al. 2013, strongly influences the predicted mass growth of intermediate and low mass galaxies.
The quasar mode controls the amount of cold gas that is fueled into the central black hole during mergers:
\( \Delta M_{\rm BH,Q}=\frac{f_{\rm BH}(M_{\rm sat}/M_{\rm cen})\,M_{\rm cold}}{1+(V_{\rm{BH}}/V_{200c})^2} \)
despite not producing any feedback it is the main channel for black hole growth.
The radio mode controls the amount of hot gas quiescently accreted by the black hole:
\(\dot{M}_{\rm{BH}}=k_{\rm{AGN}} \left(\frac{M_{\rm{hot}}}{10^{11}M_{\odot}}\right)\left(\frac{M_{\rm{BH}}}{10^8M_{\odot}}\right)\)
this accretion is assumed to produce relativistic jets which deposit energy into the hot halo and prevent cooling.
When galaxies cross the virial radius of their companions, becoming satellites, a number of environmental processes start affecting them. These include ram-pressure and tidal striping and the lack of primordial infall. In the current version of the model we switch off ram-pressure striping in low mass groups \(\left(M_{200c}<10^{14}\right)\) . In groups of higher masses this effect is calculated as in Guo et al. 2013, by calculating the radius at which the ram-pressure forces equals the gravitational force of the satellite:
\( \rho_{\rm{sat}}\left(R_{\rm{r.p.}}\right) V_{\rm{sat}}^2=\rho_{\rm{par}}\left(R\right)V_{\rm{orbit}}^2\)
When a galaxy looses its dark matter host halo a dynamical friction merger clock is started, to calculate how long it will take for the galaxy to merge:
\(t_{\rm{friction}}=\alpha_{\rm{friction}} \frac{V_{200c}r_{\rm{sat}}^2}{GM_{\rm{sat}}\rm{ln}\Lambda}\)
After this point, the position of the galaxy is given by the position of the most-bound particle of its halo at the time it was lost, shrunk in proportion to the time elapsed.